1、给定一个复变函数:
f[z_]:=z^2+0.365-0.7I
我们就来研究这个函数的迭代过程:
NestList[f,0,20]
初值为0时,迭代10次之后,得到的复数迅速远离远点。

2、要实现可视化,可以在实平面上,象征性的画出这些点。
这就需要分别求出这些点的实部和虚部:
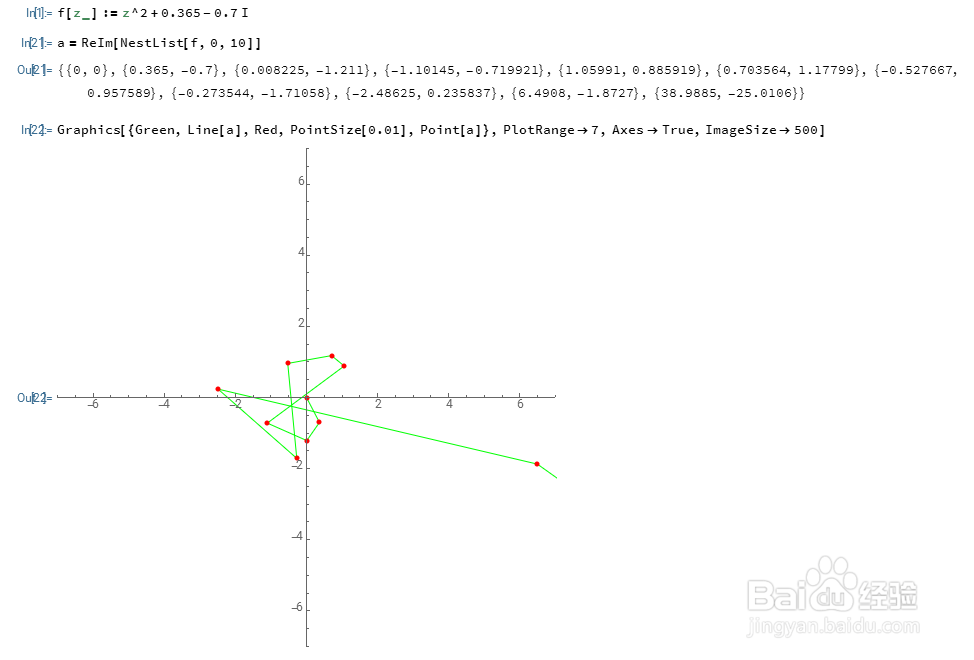
a=ReIm[NestList[f,0,10]]

3、作图:
Graphics[{Green,Line[a],Red,PointSize[0.01],Point[a]},PlotRange->7]
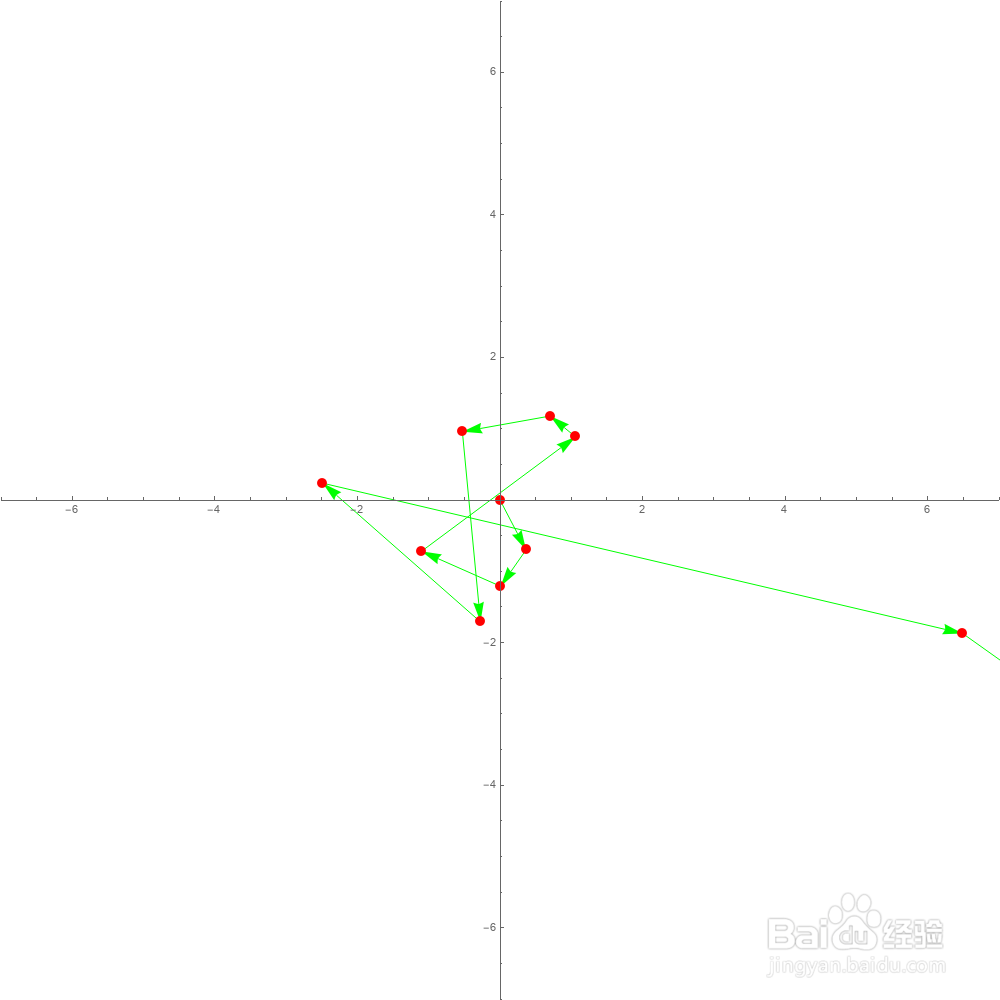
4、用箭头代替线段:
Graphics[{Green,Arrowheads[0.02],Arrow[Partition[a,2,1]],Red,PointSize[0.01],Point[a]},PlotRange->7]
得到的图片如下:
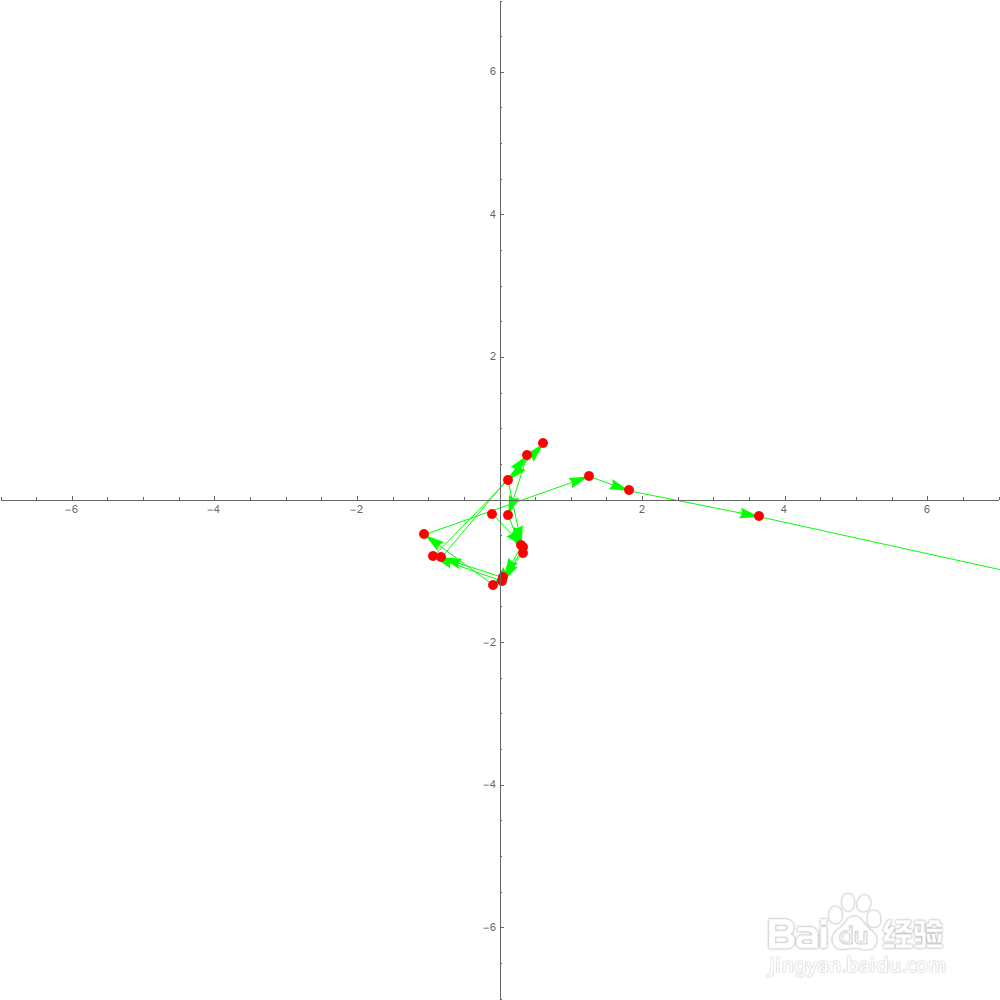
5、如果初值改为-0.1-0.2*I,那么:
a=ReIm[NestList[f,-0.1-0.2I,20]];
这时候发散的比较慢,但也是会发散的。
6、初值为-0.092-0.195I,发散过程如下:
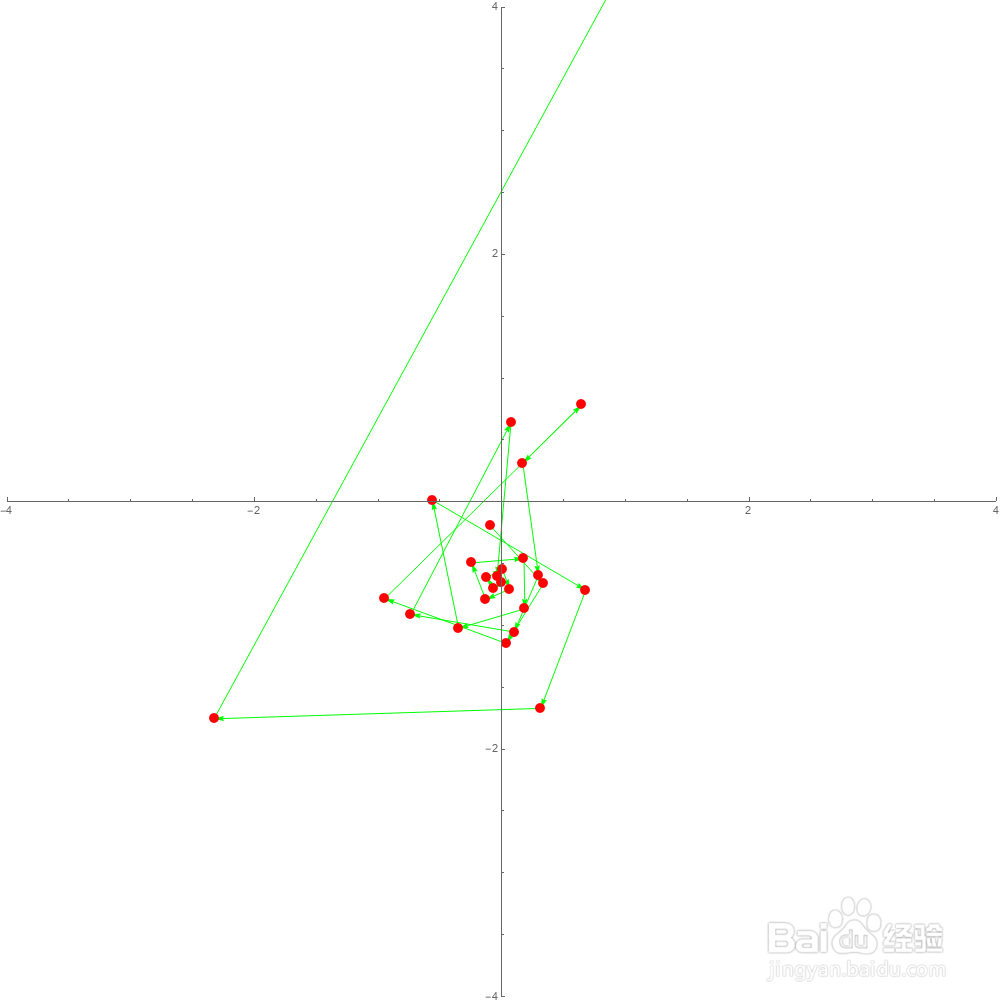
7、这样寻找不发散的初值,实在是效率太低。
我们可以转而寻找不动点,比如满足f[f[z]]=z的复数z:
b=ReIm[Solve[Nest[f,z,2]==z,z]//Values//Flatten]

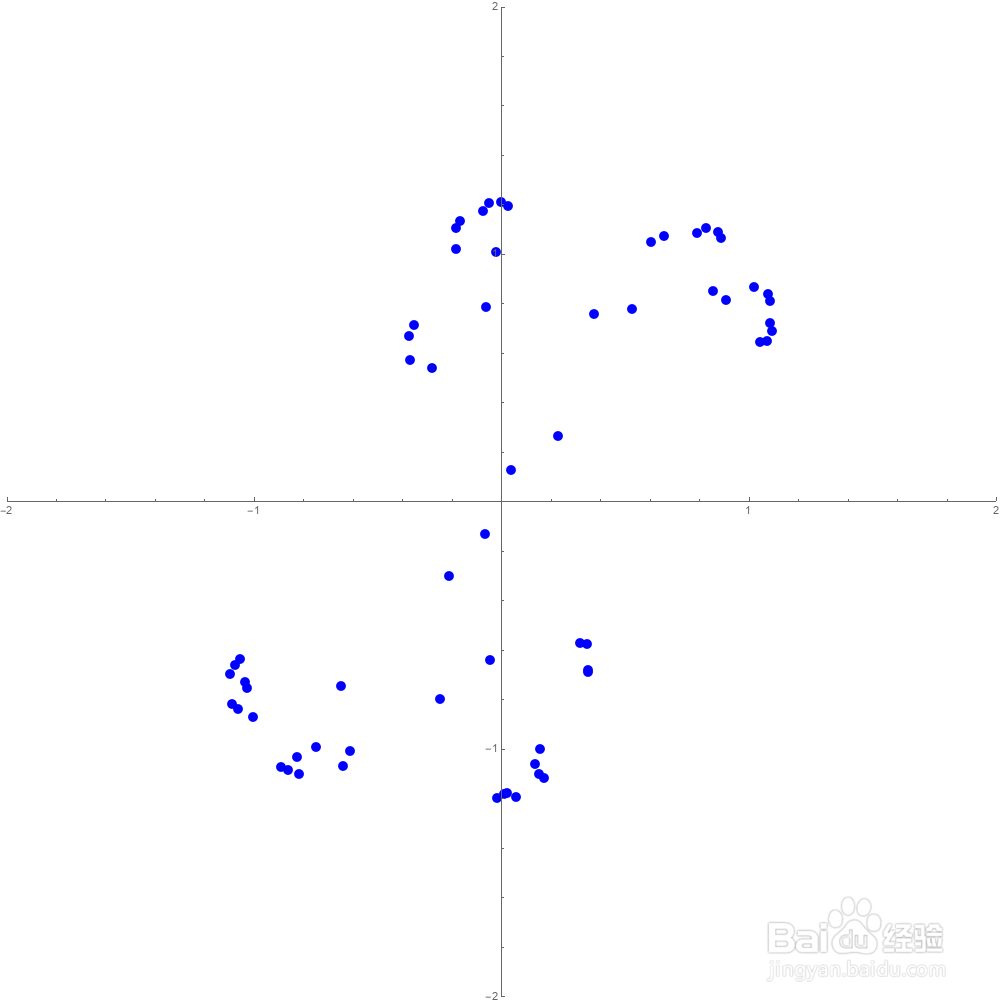
8、我们可以画出这些点:
Graphics[{Blue,PointSize[0.01],Point[b]},Axes->True,PlotRange->2]
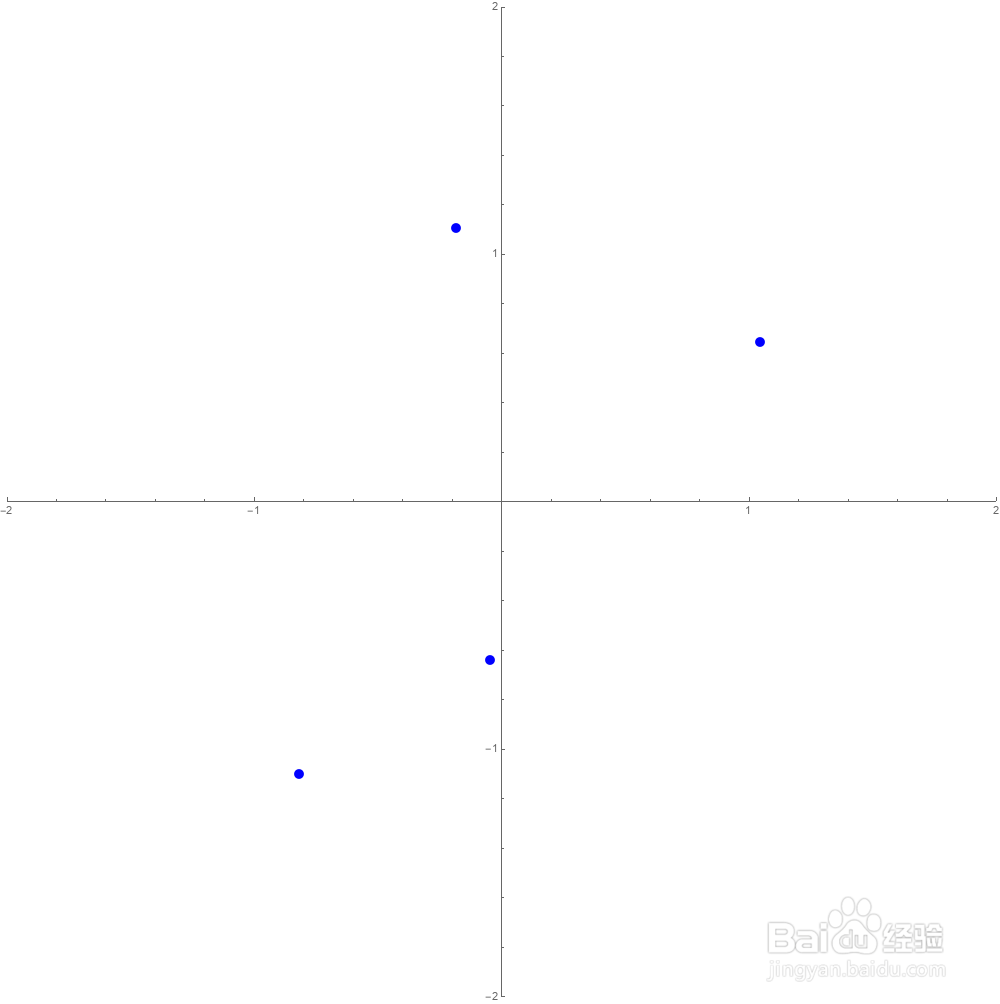
9、满足Nest[f,z,2]==z的复数有八个:
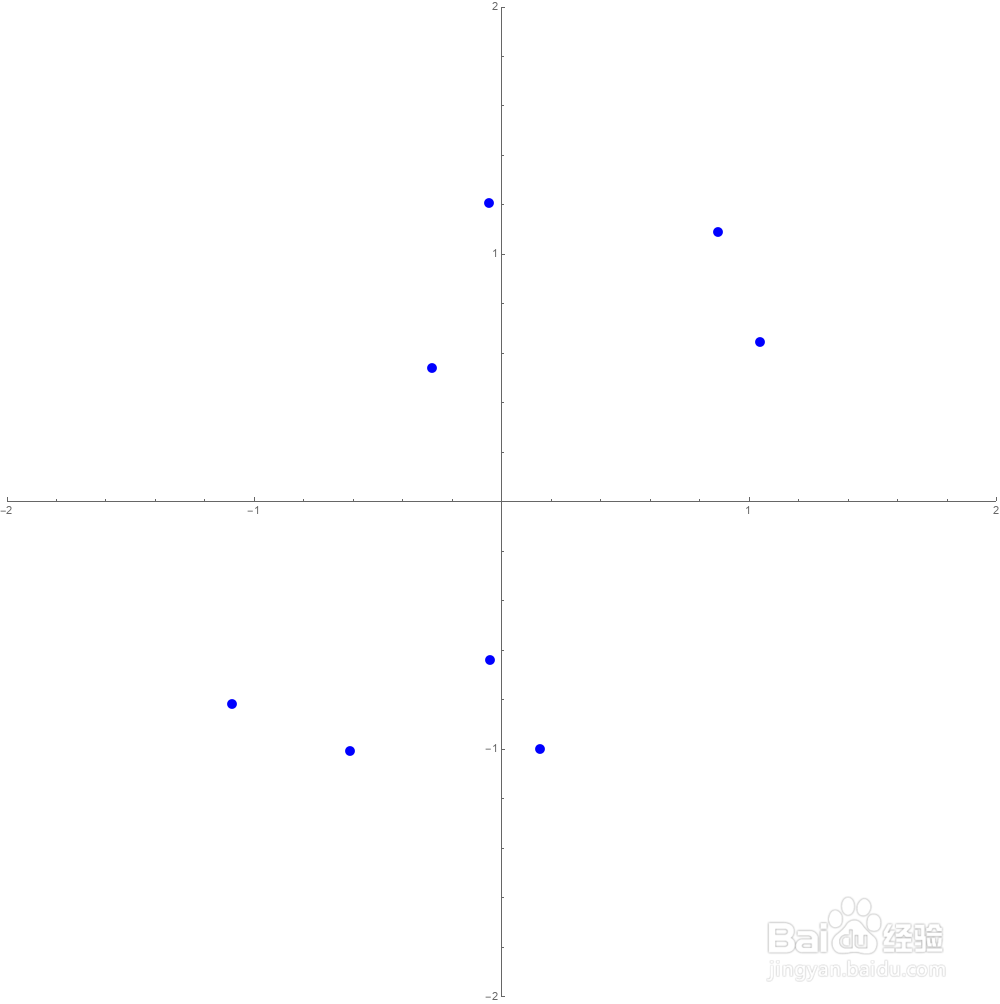
10、满足Nest[f,z,6]==z的复数有2^6个: