根据一道例题辔亿呶邂说明解法。
例:求函数y=√(x+1)-x的最大值。
解:①求出该函数定义域:x+1≥0,故x≥-1;
②将该函数拆分为两个简单函数相减形式,即令y₁=√(x+1),y₂=x,则y=y₁-y₂;
③建立平面直角坐标系,将两个简单函数的图像绘制在同一个坐标系中,如下图:(注意须截取原函数定义域内部分)
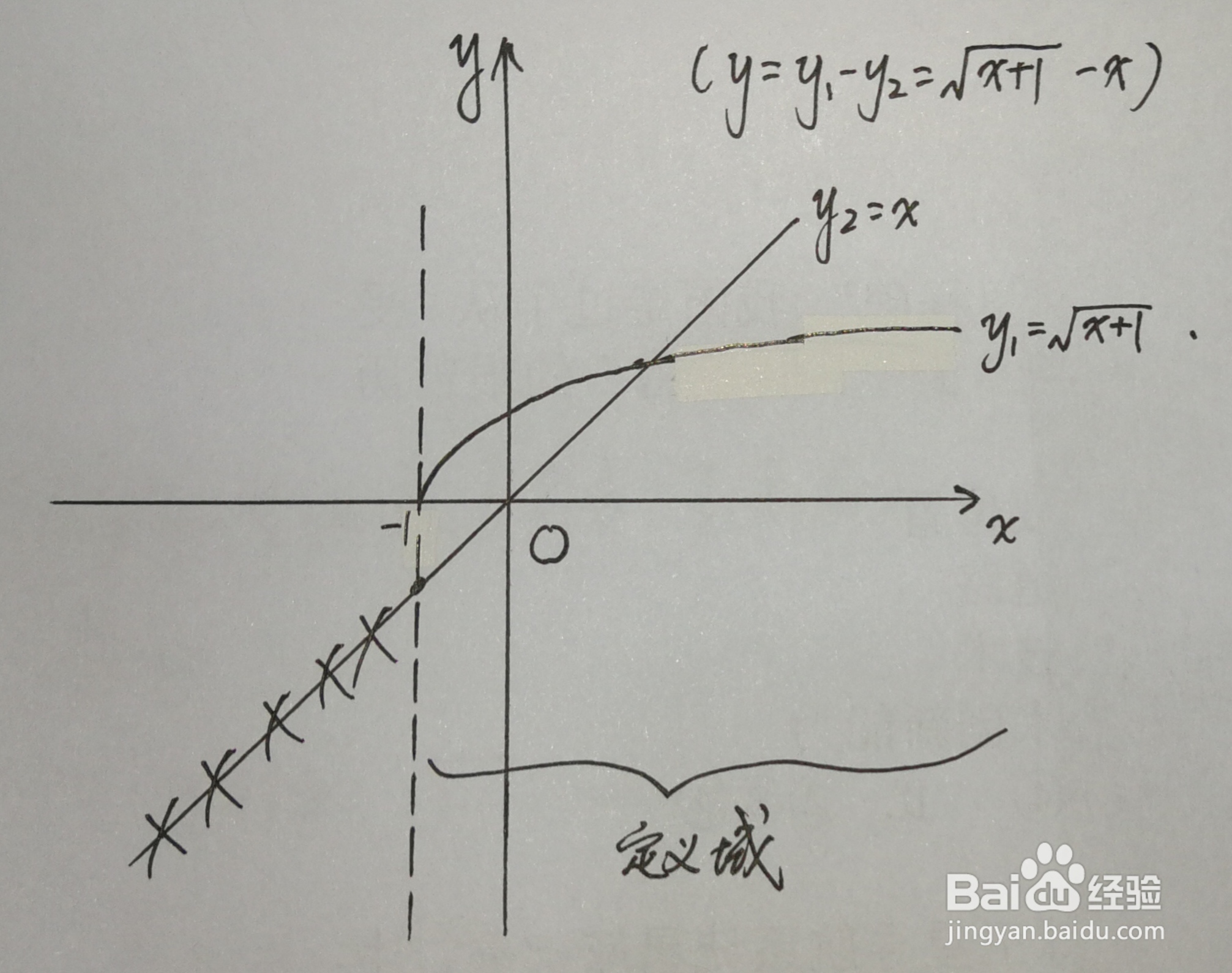
④观察图像找出两函数关系(此步骤不需要落笔):
A.找特殊点(特殊的横坐标值或函数图像交点等):当x=-1时,y₁=0,y₂=-1,y=1;当x=0时,y₁=1,y₂=0,y=1;两函数图像交点横坐标为(1+√5)/2;
B.找函数图像变化趋势及关系(需要一定的图像感知能力):当-1≤x≤(1+√5)/2时,y的值先变大后变小,又∵f(-1)=f(0)=1,∴该范围内最大值对应横坐标在-1和0之间;x>(1+√5)/2时,y₂函数图像在y₁图像上方,故y₁
⑤平移其中一个函数至与另一个函数相切:将y₂向上平移至与y₁相切于点P,设平移后为y₃=y₂+k=x+k,且k>0;(对于平移哪个函数图像没有具体规定,视具体情况而定,一般平移较为简单的函数的图像)
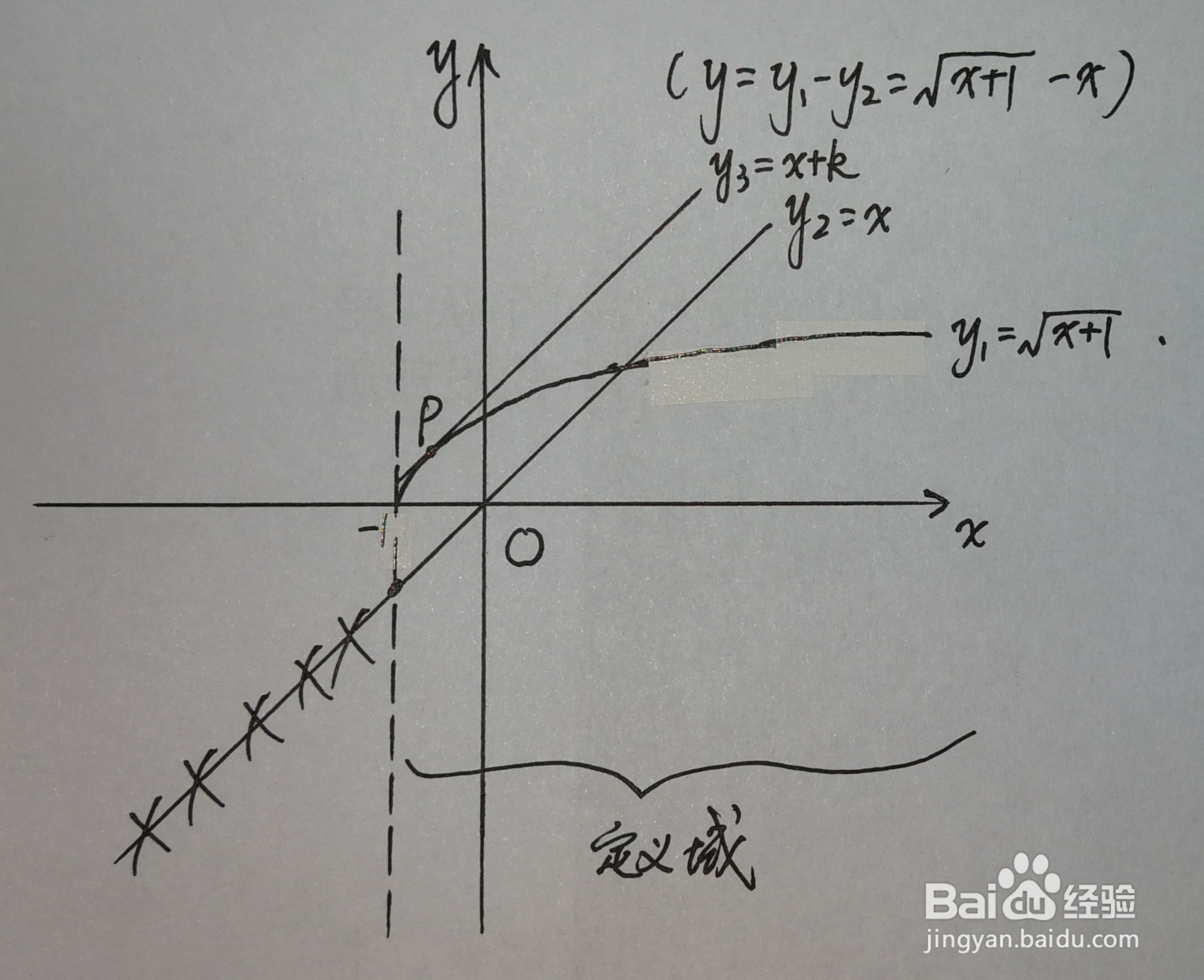
⑥联立y₁与y₃,x+k=√(x+1),x²+(2k-1)x+k²-1=0,∵两函数图像相切,只有一个交点,∴Δ=(2k-1)²-4(k²-1)=0,解得:k=5/4;将k的值代入原方程,得:x²+3/2x+9/16=0,解得:x=-3/4,故P点横坐标为-3/4;
⑦将切点横坐标代入原函数:当x=-3/4时,y=5/4,故函数y=√(x+1)-x的最大值为5/4。
总结:求定义域→拆分函数→绘制图像→找关系→平移相切→联立解方程(Δ=0)→代回原函数。
说明:若复杂函数为两个简单函数相减的形式,即可参照上述步骤;若为两个简单函数相加的形式,如y=2/x+√x,则需先转化为两个简单函数相减形式,即变成y=√x-(-2/x)或y=2/x-(-√x),再参照上述步骤。
