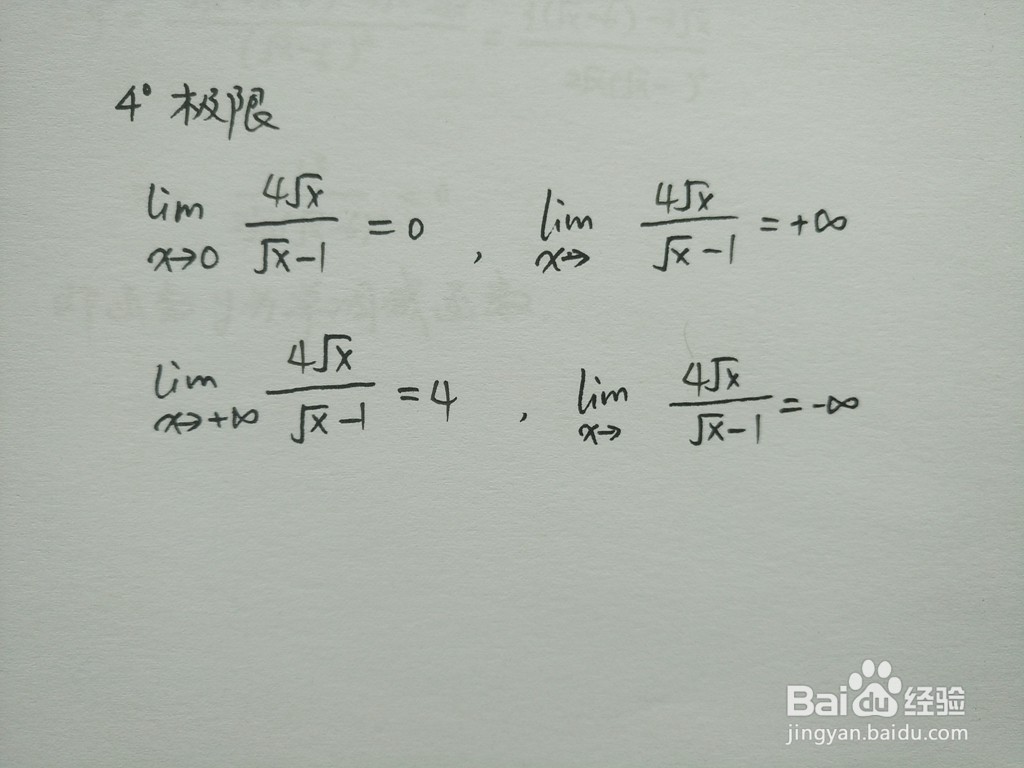1、函数的定义域,根据根式定义域和分母不为0的要求,求出函数的定义域。

2、 定义域是指该函数的有效范围,函数的定义域就是使得这个函数关系式有意义的实数的全体构成的集合。
3、用导数的知识判断函数的单调性,求出函数的一阶导数,根据一阶导数小于0,即可判断函数的单调性为减函数。

4、在利用导数讨论函数的单调区间时,首先要确定函数的定义域,解决问题的过程中只能在定义域内,通过讨论导数的符号来判断函数的单调区间。
5、先求出函数的二阶导数,再求出函数的驻点,根据驻点判断二阶导数的符号,即可分析函数的凸凹性,进而求出函数的凸凹区间。

6、函数的极限计算。