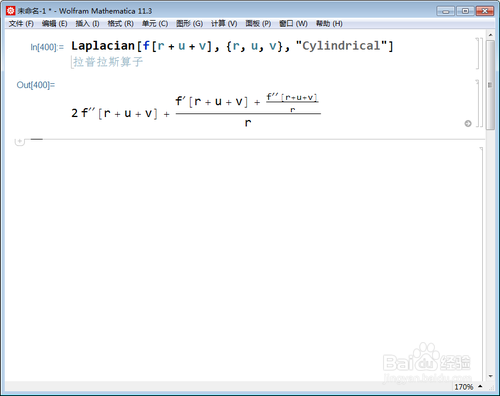
1、Laplacian[Sin[r + u], {r, u}, "Polar"]
把r视为极径、u视为极角:
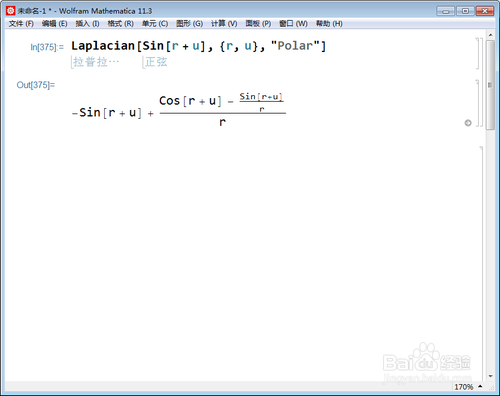
2、Laplacian[f[r + u], {r, u}, "Polar"]
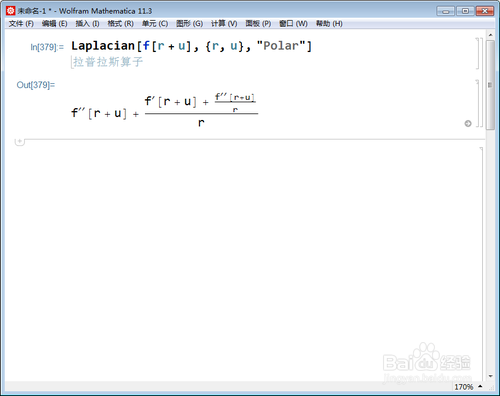
3、Laplacian[f[r], {r, u}, "Polar"]
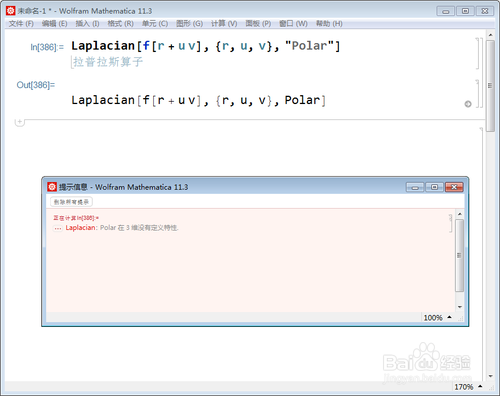
4、"Polar"只适用于二元情形:
Laplacian[f[r + u v], {r, u, v}, "Polar"]
这导致报错。
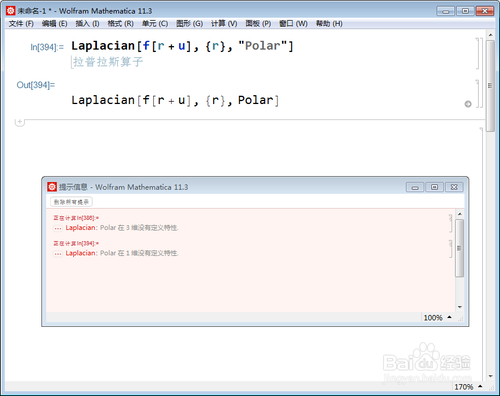
5、Laplacian[f[r + u], {r}, "Polar"]
这也报错。
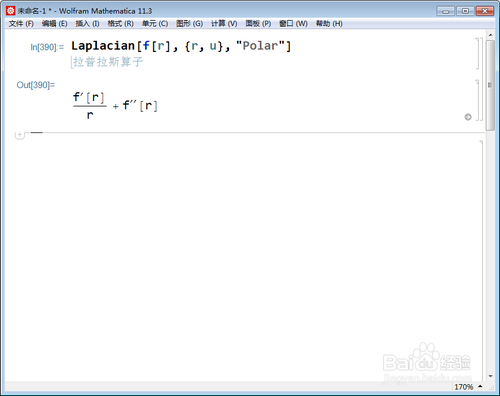
6、与极坐标相对应的三维模式是柱坐标:
Laplacian[f[r + u + v], {r, u, v}, "Cylindrical"]